Ecuación de segundo grado
Una ecuación de segundo grado1 2 o ecuación cuadrática de una variable es una ecuación algebraica que conlleva una expresión algebraica de términos cuyo grado máximo es dos, es decir, una ecuación cuadrática puede ser representada por untrinomio de segundo grado o binomio de segundo grado. La expresión general de una ecuación cuadrática de una variable es:
donde x representa la variable, y donde a, b y c son constantes[cita requerida]; a es el coeficiente cuadrático (distinto de 0), b el coeficiente lineal y c es el término independiente. Este polinomio, si los coeficientes son números reales, se puede representar mediante la gráfica de una función cuadrática, es decir, por una parábola. Esta representación gráfica es útil, porque las intersecciones de esta gráfica, en el caso de existir, con el eje X coinciden con las soluciones reales de la ecuación.
A la variable x, algunos llaman indeterminada3 otros llaman incógnita.
Definición en el dominio de los reales[editar]
Una ecuación algebraica se puede plantear en diferentes conjuntos numéricos. Justamente alguien dice con polinomios con coeficientes en ℂ 5 . Sin embargo se presenta en el caso que se trabaje en ℝ.
Una ecuación cuadrática se puede escribir en la forma:donde son números reales y
. En la actualidad la herramienta principal para la resolución de tales ecuaciones es la factorizazión . Si la ecuación se reduce a
se llama cuadrática pura y se puede resolver hallando las raíces cuadradas de un único número real. Si las raíces son imaginarias .
Historia[editar]
El origen y la solución de las ecuaciones de segundo grado son de gran antigüedad. En Babilonia se conocieron algoritmos para resolverla.Fue encontrado independientemente en otros lugares del mundo. En Grecia, el matemático Diofanto de Alejandría aportó un procedimiento para resolver este tipo de ecuaciones (aunque su método sólo proporcionaba una de las soluciones, incluso en el caso de que las dos soluciones sean positivas). La primera solución completa la desarrolló el matemático Al-Juarismi (o Al-Khwarizmi según otras grafías), en el siglo IX en su trabajo Compendio de cálculo por reintegración y comparación, cerrando con ello un problema que se había perseguido durante siglos. Basándose en el trabajo de Al-Juarismi, el matemático judeoespañol Abraham bar Hiyya, en su Liber embadorum, discute la solución de estas ecuaciones.[cita requerida] Hay que esperar a Évariste Galois para conseguir resolver en general las ecuaciones polinómicas, o saber cuándo son irresolubles por radicales, que viene a ser una generalización de los métodos de resolución de las ecuaciones de segundo grado.
- La primera gran dificultad que surgió en la solución de ecuaciones cuadráticas se dio con la ecuación
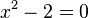 en la época de los pitagóricos, al calcular la longitud de la diagonal de un cuadrado de lado 1.No se podía expresar la raíz cuadrada de dos como razón de dos números enteros. 7 . Lo que permitió la formulación de números irracionales.
en la época de los pitagóricos, al calcular la longitud de la diagonal de un cuadrado de lado 1.No se podía expresar la raíz cuadrada de dos como razón de dos números enteros. 7 . Lo que permitió la formulación de números irracionales. - Luego , ya en el Renacimiento, al resolver
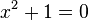 , pues exige hallar un número real cuyo cuadrado sea -1; y se sabe que el cuadrado de cualquier real es positivo; lo que se superó con la adopción de números imaginarios y la definición de la unidad imaginaria i que cumple
, pues exige hallar un número real cuyo cuadrado sea -1; y se sabe que el cuadrado de cualquier real es positivo; lo que se superó con la adopción de números imaginarios y la definición de la unidad imaginaria i que cumple
Fórmula cuadrática[editar]
Para una ecuación cuadrática con coeficientes reales o complejos existen siempre dos soluciones, no necesariamente distintas, llamadas raíces, que pueden ser reales o complejas (si los coeficientes son reales y existen dos soluciones no reales, entonces deben ser complejas conjugadas). Fórmula general para la obtención de raíces:
Se usa ± para indicar las dos soluciones:
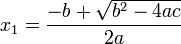
y 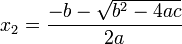
| [Expandir]Deducción de la solución |
Discriminante[editar]
.
En la fórmula anterior, la expresión dentro de la raíz cuadrada recibe el nombre de discriminante de la ecuación cuadrática. Suele representarse con la letra D o bien con la letra griega Δ (delta) en mayúscula:
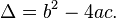
Una ecuación cuadrática con coeficientes reales tiene o bien dos soluciones reales distintas o una sola solución real demultiplicidad 2, o bien dos raíces complejas. El discriminante determina la índole y la cantidad de raíces.
- Si
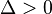 hay dos soluciones reales y diferentes (la parábola cruza dos veces el eje de las abscisas: X):
hay dos soluciones reales y diferentes (la parábola cruza dos veces el eje de las abscisas: X):
-
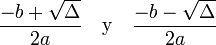 .
.
- Si
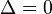 hay una solución real doble (la parábola sólo toca en un punto al eje de las abscisas: X):
hay una solución real doble (la parábola sólo toca en un punto al eje de las abscisas: X):
- Si
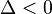 hay dos soluciones complejas conjugadas (la parábola no corta al eje de las abscisas: X):
hay dos soluciones complejas conjugadas (la parábola no corta al eje de las abscisas: X):



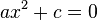


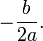
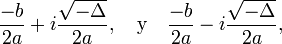
No hay comentarios:
Publicar un comentario